Bivariate Probit model

biprobit(
  x,
  data,
  id,
  rho = ~1,
  num = NULL,
  strata = NULL,
  eqmarg = TRUE,
  indep = FALSE,
  weights = NULL,
  weights.fun = function(x) ifelse(any(x <= 0), 0, max(x)),
  randomeffect = FALSE,
  vcov = "robust",
  pairs.only = FALSE,
  allmarg = !is.null(weights),
  control = list(trace = 0),
  messages = 1,
  constrain = NULL,
  table = pairs.only,
  p = NULL,
  ...
)

Arguments

x: formula (or vector)
data: data.frame
id: The name of the column in the dataset containing the cluster id-variable.
rho: Formula specifying the regression model for the dependence parameter
num: Optional name of order variable
strata: Strata
eqmarg: If TRUE same marginals are assumed (exchangeable)
indep: Independence
weights: Weights
weights.fun: Function defining the bivariate weight in each cluster
randomeffect: If TRUE a random effect model is used (otherwise correlation parameter is estimated allowing for both negative and positive dependence)
vcov: Type of standard errors to be calculated
pairs.only: Include complete pairs only?
allmarg: Should all marginal terms be included
control: Control argument parsed on to the optimization routine. Starting values may be parsed as 'start'.
messages: Control amount of messages shown
constrain: Vector of parameter constraints (NA where free). Use this to set an offset.
table: Type of estimation procedure
p: Parameter vector p in which to evaluate log-Likelihood and score function
...: Optional arguments

Examples

data(prt)
prt0 <- subset(prt,country=="Denmark")
a <- biprobit(cancer~1+zyg, ~1+zyg, data=prt0, id="id")
b <- biprobit(cancer~1+zyg, ~1+zyg, data=prt0, id="id",pairs.only=TRUE)
predict(b,newdata=lava::Expand(prt,zyg=c("MZ")))
#>           p11        p10        p01       p00         p1         p2       mu1
#> 1 0.005847975 0.01052632 0.01052632 0.9730994 0.01637429 0.01637429 -2.135152
#>         mu2       rho parameter zyg
#> 1 -2.135152 0.7568562         1  MZ
predict(b,newdata=lava::Expand(prt,zyg=c("MZ","DZ")))
#>           p11        p10        p01       p00         p1         p2       mu1
#> 1 0.005847975 0.01052632 0.01052632 0.9730994 0.01637429 0.01637429 -2.135152
#> 2 0.000655527 0.01425761 0.01425761 0.9708293 0.01491313 0.01491313 -2.172390
#>         mu2       rho parameter zyg
#> 1 -2.135152 0.7568562         1  MZ
#> 2 -2.172390 0.1960491         2  DZ

 ## Reduce Ex.Timings
n <- 2e3
x <- sort(runif(n, -1, 1))
y <- rmvn(n, c(0,0), rho=cbind(tanh(x)))>0
d <- data.frame(y1=y[,1], y2=y[,2], x=x)
dd <- fast.reshape(d)

a <- biprobit(y~1+x,rho=~1+x,data=dd,id="id")
summary(a, mean.contrast=c(1,.5), cor.contrast=c(1,.5))
#> 
#>                 Estimate    Std.Err       Z p-value    
#> (Intercept)   -0.0007775  0.0196148 -0.0396  0.9684    
#> x             -0.0678344  0.0334067 -2.0306  0.0423 *  
#> r:(Intercept) -0.0407609  0.0378575 -1.0767  0.2816    
#> r:x            0.9494564  0.0715105 13.2772  <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> logLik: -2665.327  mean(score^2): 1.792e-05 
#>     n pairs 
#>  4000  2000 
#> 
#> Contrast:
#> 	Dependence    [(Intercept)] + 0.5[x] 
#> 	Mean          [(Intercept)] + 0.5[x] 
#> 
#>                         Estimate 2.5%    97.5%  
#> Rel.Recur.Risk          1.28318  1.21593 1.35042
#> OR                      3.00120  2.32822 3.86870
#> Tetrachoric correlation 0.40863  0.32083 0.48947
#>                                                 
#> Concordance             0.30328  0.27669 0.33127
#> Casewise Concordance    0.62383  0.58829 0.65809
#> Marginal                0.48616  0.46295 0.50943
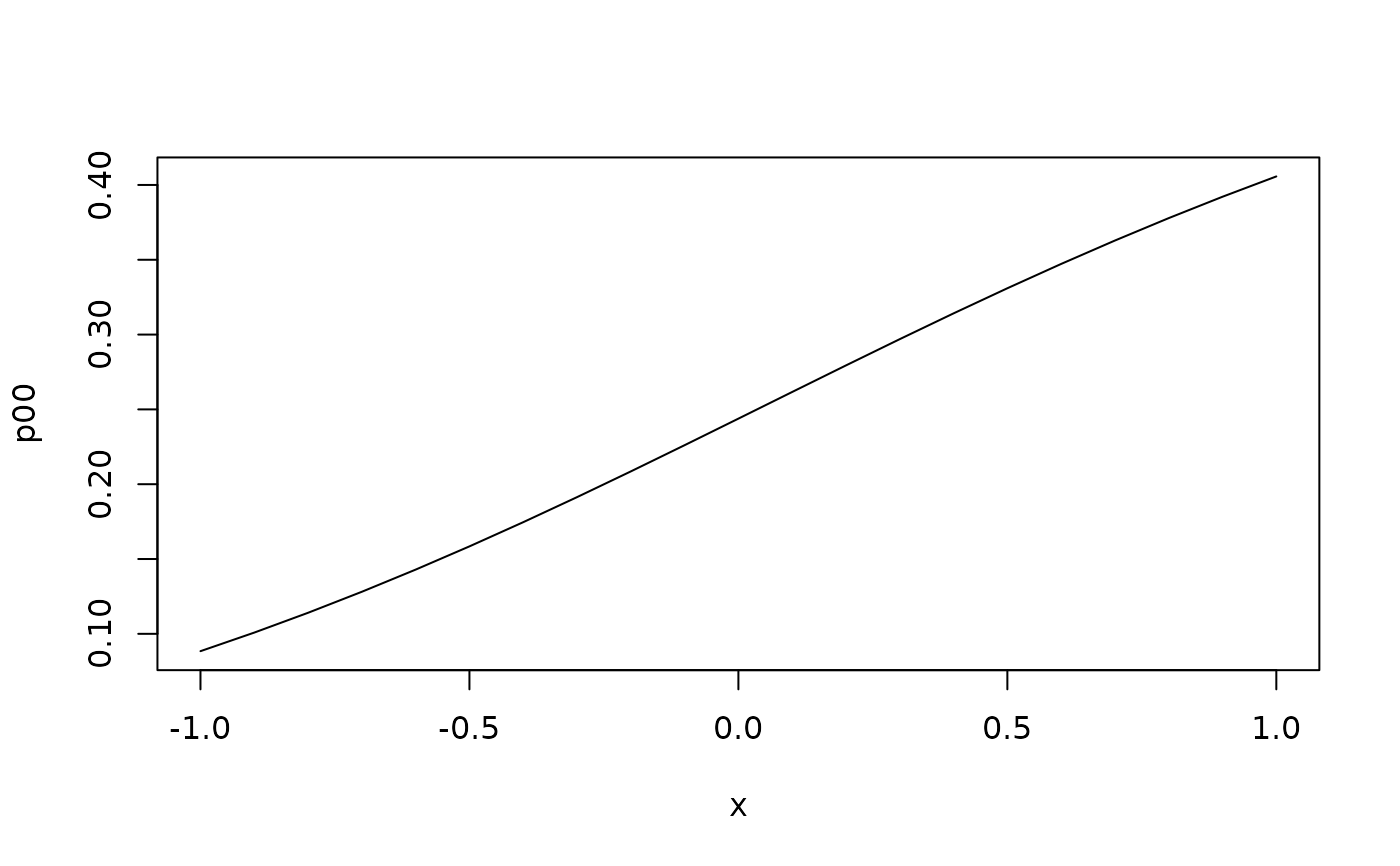
with(predict(a,data.frame(x=seq(-1,1,by=.1))), plot(p00~x,type="l"))


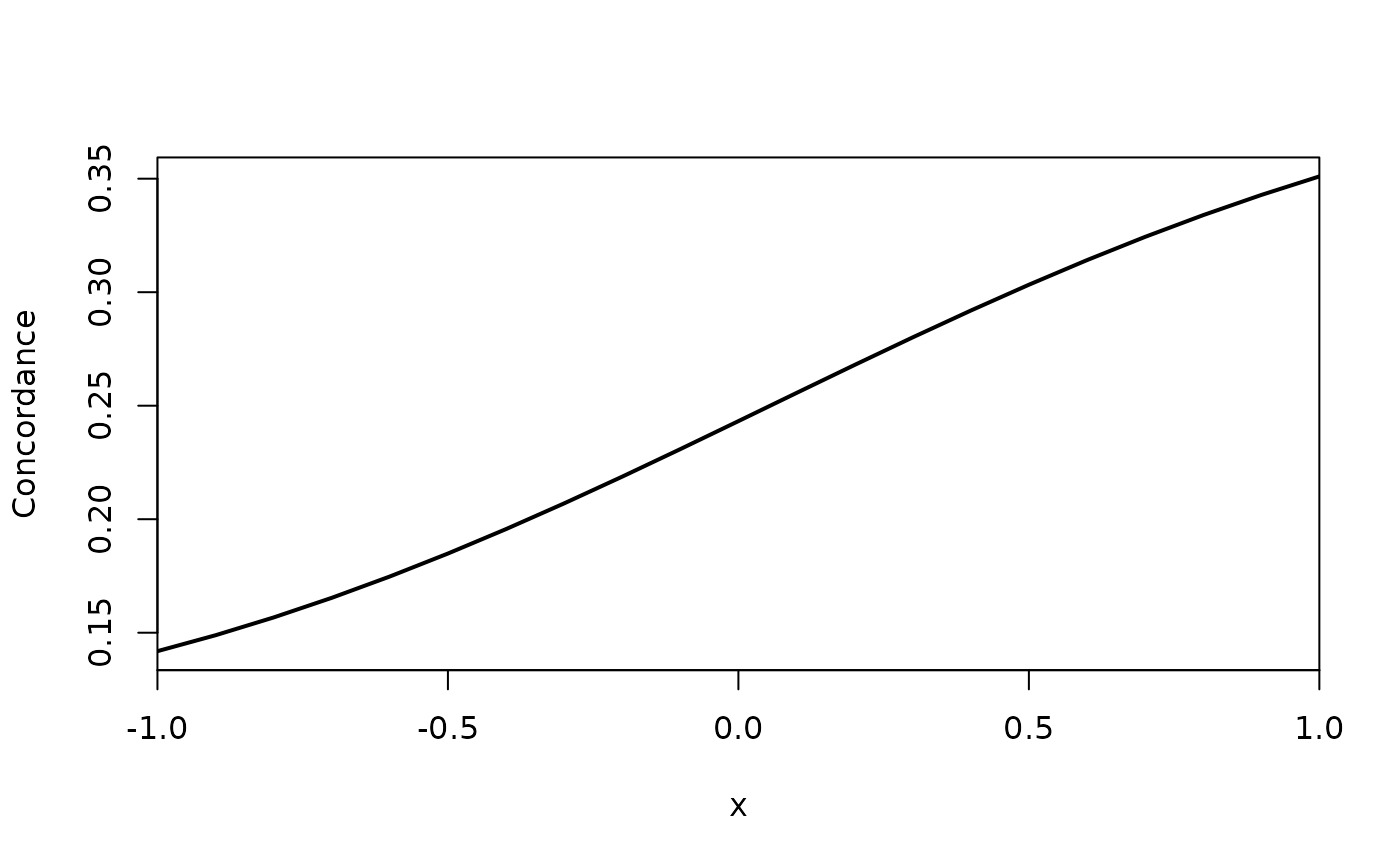
pp <- predict(a,data.frame(x=seq(-1,1,by=.1)),which=c(1))
plot(pp[,1]~pp$x, type="l", xlab="x", ylab="Concordance", lwd=2, xaxs="i")
lava::confband(pp$x,pp[,2],pp[,3],polygon=TRUE,lty=0,col=lava::Col(1))


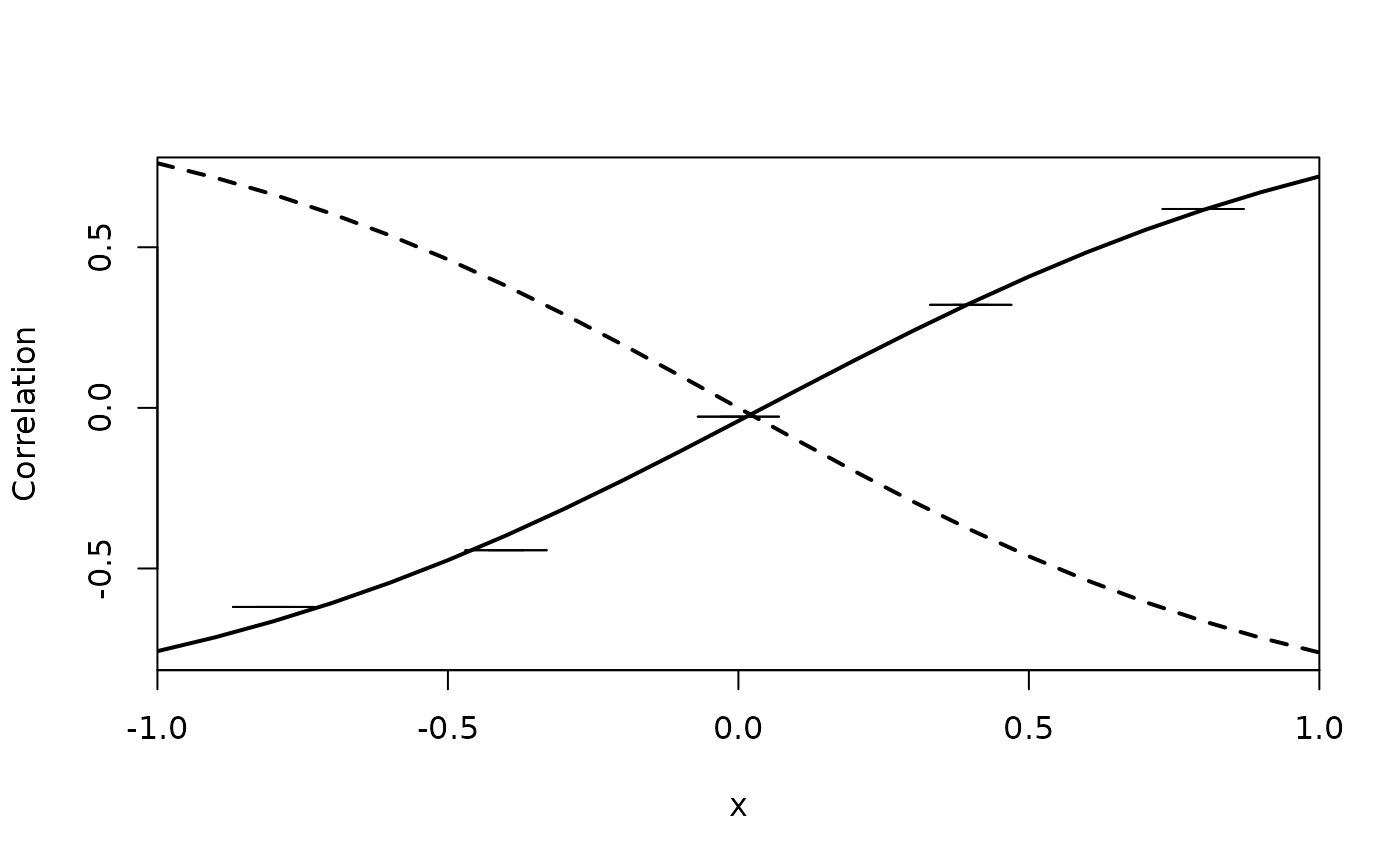
pp <- predict(a,data.frame(x=seq(-1,1,by=.1)),which=c(9)) ## rho
plot(pp[,1]~pp$x, type="l", xlab="x", ylab="Correlation", lwd=2, xaxs="i")
lava::confband(pp$x,pp[,2],pp[,3],polygon=TRUE,lty=0,col=lava::Col(1))
with(pp, lines(x,tanh(-x),lwd=2,lty=2))

xp <- seq(-1,1,length.out=6); delta <- mean(diff(xp))
a2 <- biprobit(y~1+x,rho=~1+I(cut(x,breaks=xp)),data=dd,id="id")
pp2 <- predict(a2,data.frame(x=xp[-1]-delta/2),which=c(9)) ## rho
lava::confband(pp2$x,pp2[,2],pp2[,3],center=pp2[,1])





## Time
if (FALSE) {
    a <- biprobit.time(cancer~1, rho=~1+zyg, id="id", data=prt, eqmarg=TRUE,
                       cens.formula=Surv(time,status==0)~1,
                       breaks=seq(75,100,by=3),fix.censweights=TRUE)

    a <- biprobit.time2(cancer~1+zyg, rho=~1+zyg, id="id", data=prt0, eqmarg=TRUE,
                       cens.formula=Surv(time,status==0)~zyg,
                       breaks=100)

    #a1 <- biprobit.time2(cancer~1, rho=~1, id="id", data=subset(prt0,zyg=="MZ"), eqmarg=TRUE,
    #                   cens.formula=Surv(time,status==0)~1,
    #                   breaks=100,pairs.only=TRUE)

    #a2 <- biprobit.time2(cancer~1, rho=~1, id="id", data=subset(prt0,zyg=="DZ"), eqmarg=TRUE,
    #                    cens.formula=Surv(time,status==0)~1,
    #                    breaks=100,pairs.only=TRUE)
}