Semiparametric Proportional odds model, that has the advantage that $$ logit(S(t|x)) = \log(\Lambda(t)) + x \beta $$ so covariate effects give OR of survival.
logitSurv(formula, data, offset = NULL, weights = NULL, ...)Arguments
- formula
formula with 'Surv' outcome (see
coxph)- data
data frame
- offset
offsets for exp(x beta) terms
- weights
weights for score equations
- ...
Additional arguments to lower level funtions
Details
This is equivalent to using a hazards model $$ Z \lambda(t) \exp(x \beta) $$ where Z is gamma distributed with mean and variance 1.
References
The proportional odds cumulative incidence model for competing risks, Eriksson, Frank and Li, Jianing and Scheike, Thomas and Zhang, Mei-Jie, Biometrics, 2015, 3, 687--695, 71,
Examples
data(TRACE)
dcut(TRACE) <- ~.
out1 <- logitSurv(Surv(time,status==9)~vf+chf+strata(wmicat.4),data=TRACE)
summary(out1)
#>
#> n events
#> 1878 958
#> coeffients:
#> Estimate S.E. dU^-1/2 P-value
#> vf 0.30049 0.22633 0.11154 0.1843
#> chf 1.26008 0.10095 0.07316 0.0000
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> vf 1.35052 0.86667 2.1045
#> chf 3.52570 2.89277 4.2971
#>
#>
gof(out1)
#> Cumulative score process test for Proportionality:
#> Sup|U(t)| pval
#> vf 42.28659 0.000
#> chf 20.75308 0.495
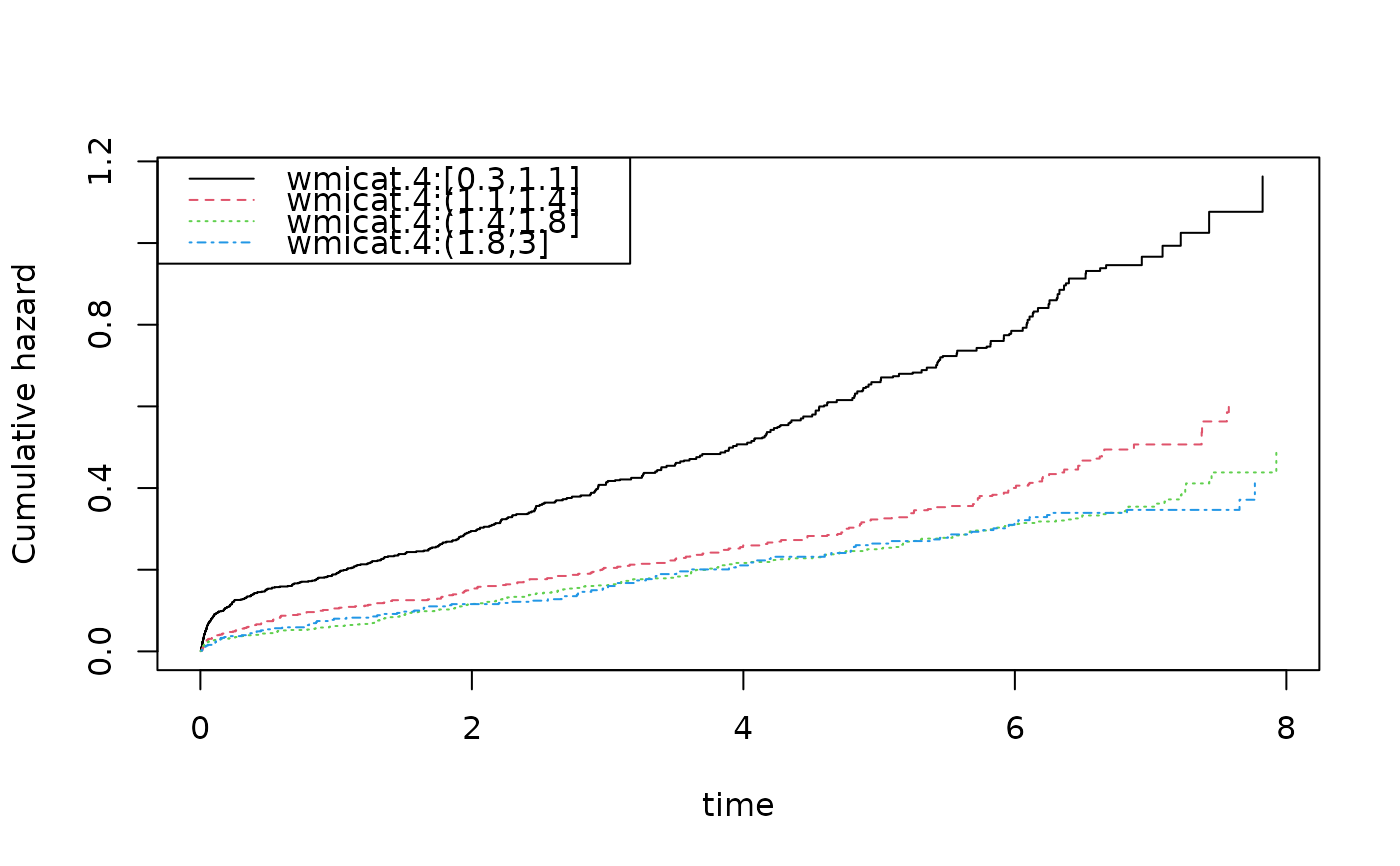
plot(out1)
