CIF logistic-link for propodds=1 default and CIF Fine-Gray (cloglog) regression for propodds=NULL. The FG model can also be called using the cifregFG function that has propodds=NULL.
cifreg(
formula,
data,
propodds = 1,
cause = 1,
cens.code = 0,
no.codes = NULL,
...
)Arguments
Details
For FG model: $$ \int (X - E ) Y_1(t) w(t) dM_1 $$ is computed and summed over clusters and returned multiplied with inverse of second derivative as iid.naive. Here $$w(t) = G(t) (I(T_i \wedge t < C_i)/G_c(T_i \wedge t))$$ and $$E(t) = S_1(t)/S_0(t)$$ and $$S_j(t) = \sum X_i^j Y_{i1}(t) w_i(t) \exp(X_i^T \beta)$$.
The iid decomposition of the beta's, however, also have a censoring term that is also is computed and added (still scaled with inverse second derivative) $$ \int (X - E ) Y_1(t) w(t) dM_1 + \int q(s)/p(s) dM_c $$ and returned as the iid
For logistic link standard errors are slightly to small since uncertainty from recursive baseline is not considered, so for smaller data-sets it is recommended to use the prop.odds.subdist of timereg that is also more efficient due to use of different weights for the estimating equations. Alternatively, one can also bootstrap the standard errors.
Examples
## data with no ties
library(mets)
data(bmt,package="timereg")
bmt$time <- bmt$time+runif(nrow(bmt))*0.01
bmt$id <- 1:nrow(bmt)
## logistic link OR interpretation
or=cifreg(Event(time,cause)~tcell+platelet+age,data=bmt,cause=1)
summary(or)
#>
#> n events
#> 408 161
#>
#> 408 clusters
#> coeffients:
#> Estimate S.E. dU^-1/2 P-value
#> tcell -0.70959 0.33198 0.27493 0.0326
#> platelet -0.45529 0.23601 0.18792 0.0537
#> age 0.39117 0.09803 0.08367 0.0001
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> tcell 0.49185 0.25659 0.9428
#> platelet 0.63426 0.39937 1.0073
#> age 1.47871 1.22023 1.7920
#>
#>
par(mfrow=c(1,2))
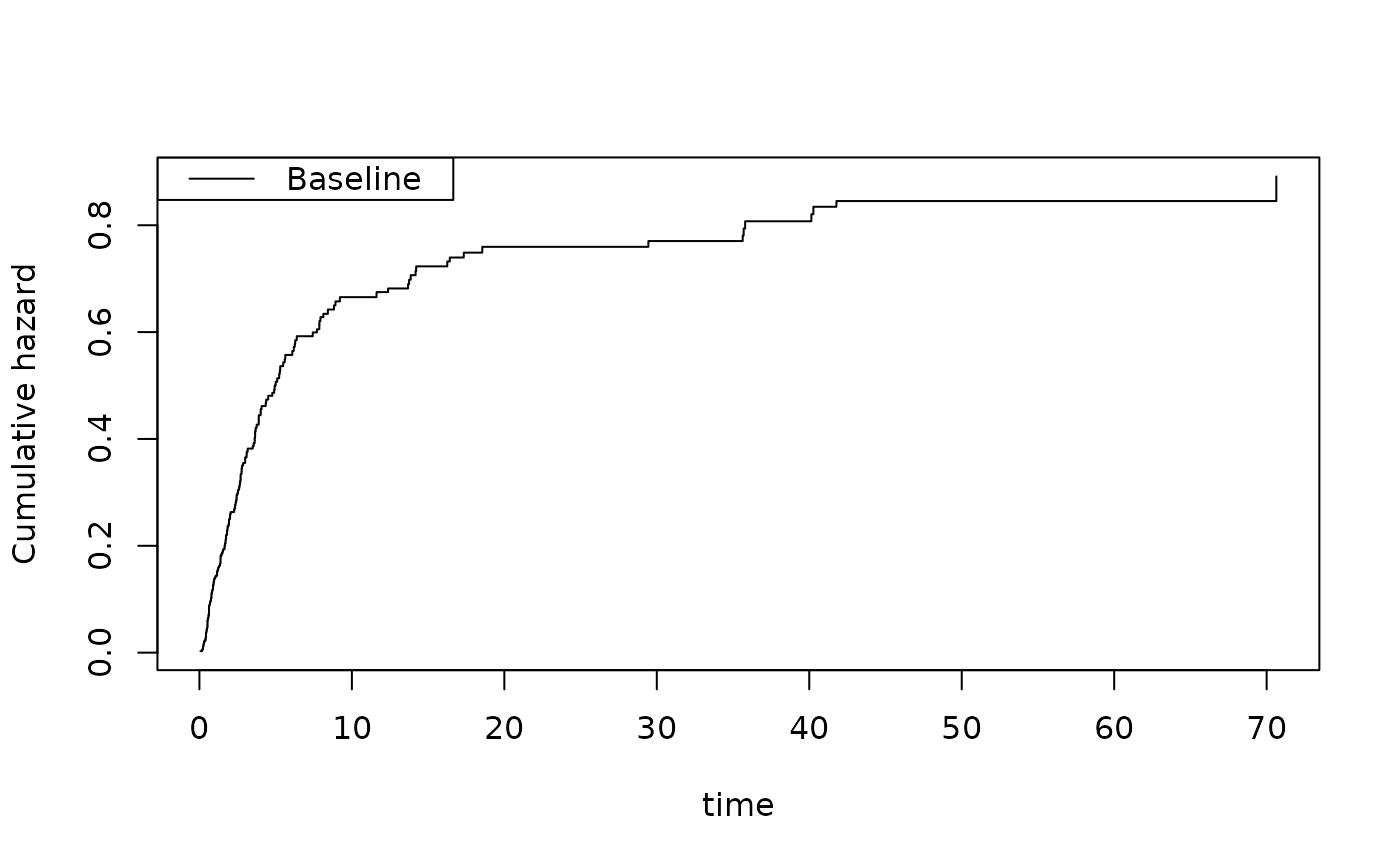
plot(or)
nd <- data.frame(tcell=c(1,0),platelet=0,age=0)
por <- predict(or,nd)
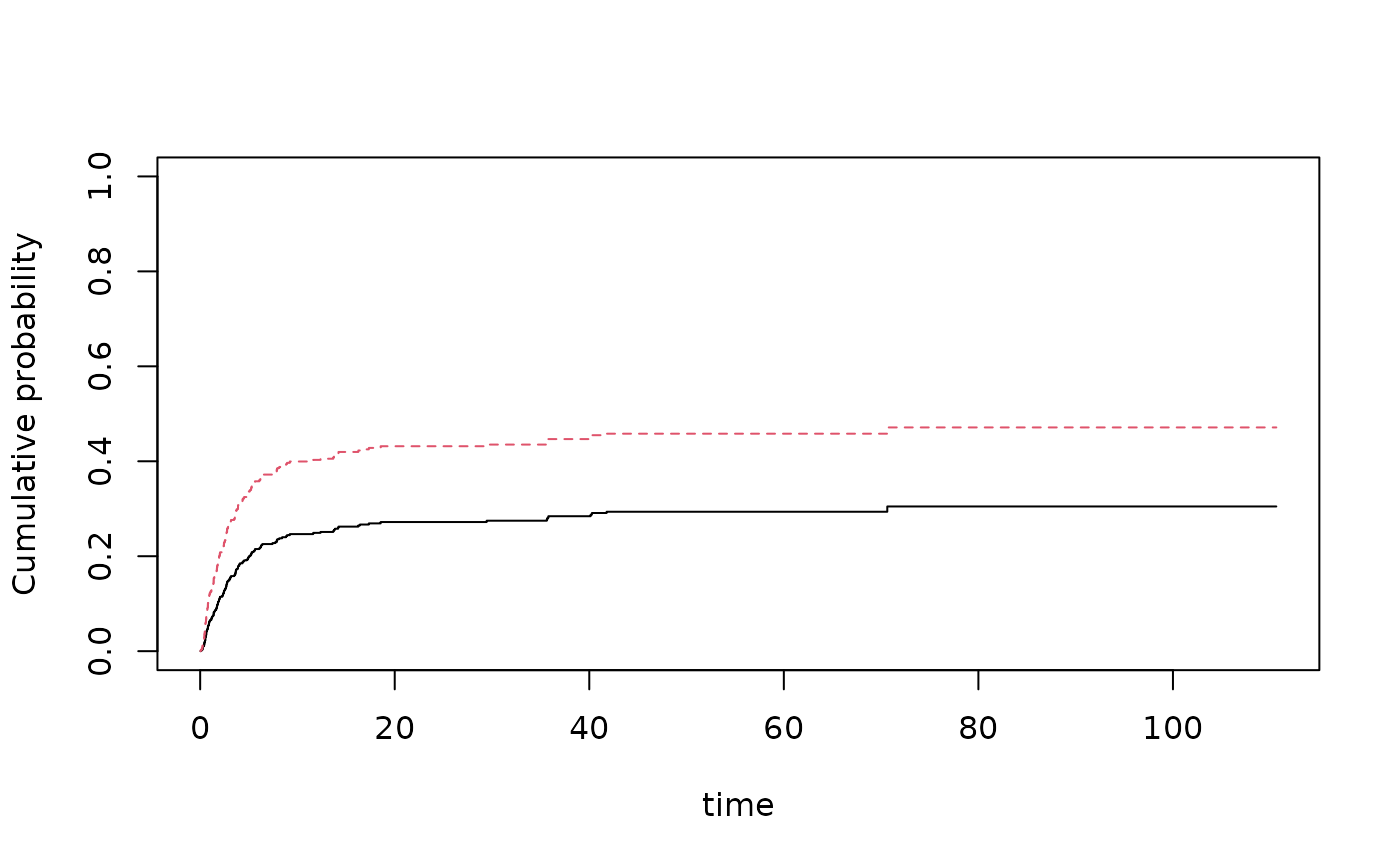
plot(por)
## Fine-Gray model
fg=cifregFG(Event(time,cause)~tcell+platelet+age,data=bmt,cause=1)
summary(fg)
#>
#> n events
#> 408 161
#>
#> 408 clusters
#> coeffients:
#> Estimate S.E. dU^-1/2 P-value
#> tcell -0.596936 0.270459 0.275783 0.0273
#> platelet -0.425847 0.180710 0.187721 0.0184
#> age 0.343870 0.080271 0.086287 0.0000
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> tcell 0.55050 0.32400 0.9353
#> platelet 0.65322 0.45839 0.9308
#> age 1.41040 1.20508 1.6507
#>
#>
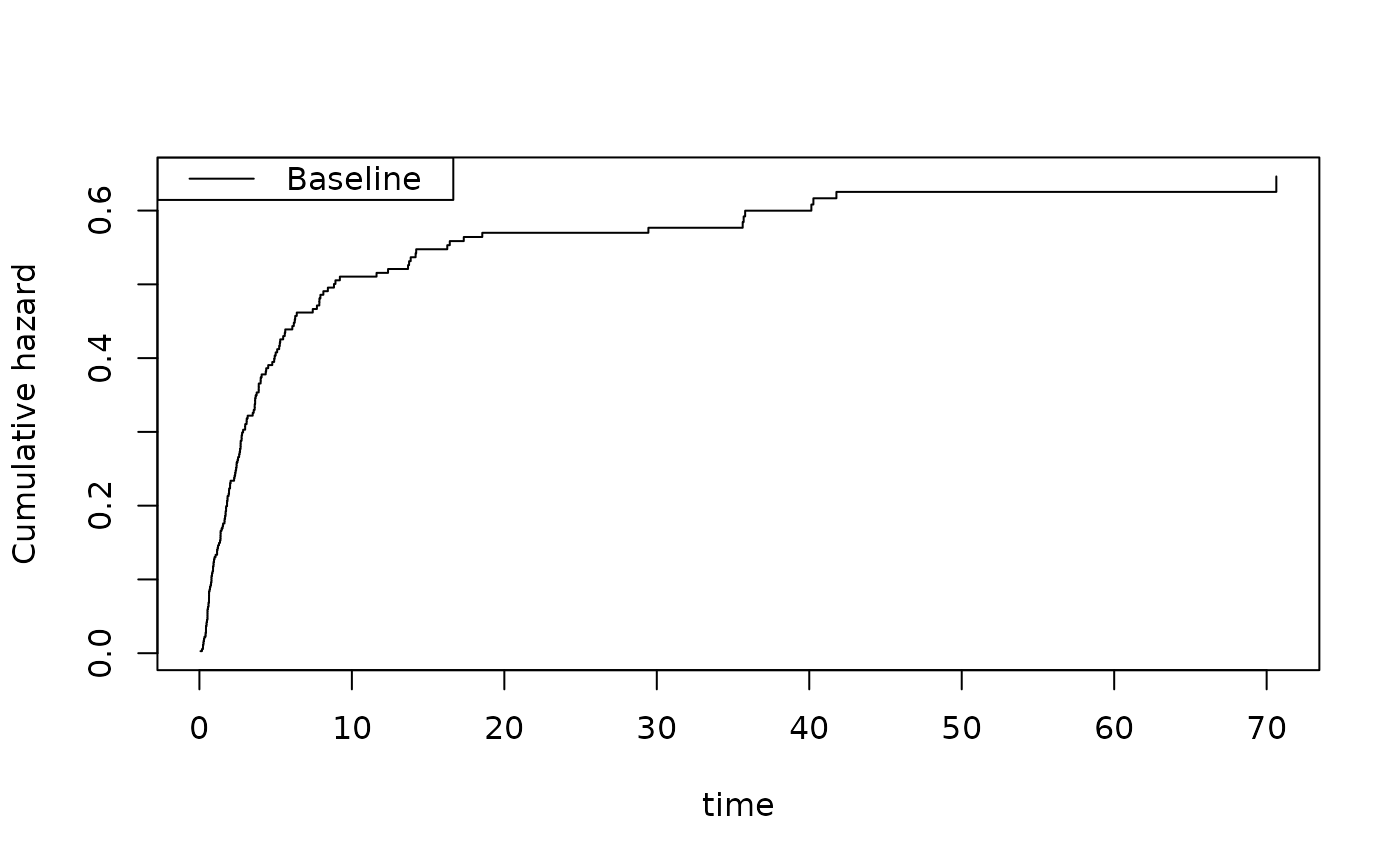
plot(fg)
nd <- data.frame(tcell=c(1,0),platelet=0,age=0)
pfg <- predict(fg,nd,se=1)
plot(pfg,se=1)
## not run to avoid timing issues
## gofFG(Event(time,cause)~tcell+platelet+age,data=bmt,cause=1)
sfg <- cifregFG(Event(time,cause)~strata(tcell)+platelet+age,data=bmt,cause=1)
summary(sfg)
#>
#> n events
#> 408 161
#>
#> 408 clusters
#> coeffients:
#> Estimate S.E. dU^-1/2 P-value
#> platelet -0.424504 0.180790 0.187822 0.0189
#> age 0.342067 0.079865 0.086287 0.0000
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> platelet 0.65409 0.45894 0.9322
#> age 1.40785 1.20386 1.6464
#>
#>
plot(sfg)
### predictions with CI based on iid decomposition of baseline and beta
### these are used in the predict function above
fg <- cifregFG(Event(time,cause)~tcell+platelet+age,data=bmt,cause=1)
Biid <- IIDbaseline.cifreg(fg,time=20)
pfg1 <- FGprediid(Biid,nd)
pfg1
#> pred se-log lower upper
#> [1,] 0.2692909 0.22757612 0.1723886 0.4206635
#> [2,] 0.4344307 0.07477437 0.3752083 0.5030006
