Simple version of comp.risk function of timereg for just one time-point thus fitting the model $$P(T \leq t, \epsilon=1 | X ) = expit( X^T beta) $$
Usage
binreg(
formula,
data,
cause = 1,
time = NULL,
beta = NULL,
type = c("II", "I"),
offset = NULL,
weights = NULL,
cens.weights = NULL,
cens.model = ~+1,
se = TRUE,
kaplan.meier = TRUE,
cens.code = 0,
no.opt = FALSE,
method = "nr",
augmentation = NULL,
outcome = c("cif", "rmst", "rmtl"),
model = c("default", "logit", "exp", "lin"),
Ydirect = NULL,
monotone = TRUE,
...
)Arguments
- formula
formula with outcome (see
coxph)- data
data frame
- cause
cause of interest (numeric variable)
- time
time of interest
- beta
starting values
- type
"II" adds augmentation term, and "I" classic binomial regression
- offset
offsets for partial likelihood
- weights
for score equations
- cens.weights
censoring weights
- cens.model
only stratified cox model without covariates
- se
to compute se's based on IPCW
- kaplan.meier
uses Kaplan-Meier for IPCW in contrast to exp(-Baseline)
- cens.code
gives censoring code
- no.opt
to not optimize
- method
for optimization
- augmentation
to augment binomial regression
- outcome
can do CIF regression "cif"=F(t|X), "rmst"=E( min(T, t) | X) , or years-lost "rmtl"=E( I(epsilon==cause) ( t - mint(T,t)) ) | X)
- model
link functions used, with defaults logit for cif, exp for rmst or rmtl, but can be logit, exp or lin (for identity link)
- Ydirect
use this Y instead of outcome constructed inside the program (e.g. I(T< t, epsilon=1)), then uses IPCW vesion of the Y, set outcome to "rmst" to fit using the model specified by model
- monotone
if true then uses del link functions used, with defaults logit for cif, exp for rmst or rmtl, but can be logit, exp or lin (for identity link)
- ...
Additional arguments to lower level funtions
Details
Based on binomial regresion IPCW response estimating equation: $$ X ( \Delta^{ipcw}(t) I(T \leq t, \epsilon=1 ) - expit( X^T beta)) = 0 $$ where $$\Delta^{ipcw}(t) = I((min(t,T)< C)/G_c(min(t,T)-)$$ is IPCW adjustment of the response $$Y(t)= I(T \leq t, \epsilon=1 )$$.
(type="I") sovlves this estimating equation using a stratified Kaplan-Meier for the censoring distribution. For (type="II") the default an additional censoring augmentation term $$X \int E(Y(t)| T>s)/G_c(s) d \hat M_c$$ is added.
logitIPCW instead considers $$ X I(min(T_i,t) < G_i)/G_c(min(T_i ,t)) ( I(T \leq t, \epsilon=1 ) - expit( X^T beta)) = 0 $$ a standard logistic regression with weights that adjust for IPCW.
When monotone is FALSE the solved equation for binreg is equivalent to minmizing the least squares problem and thus becomes $$ D_\beta h(\beta) ( \Delta^{ipcw}(t) I(T \leq t, \epsilon=1 ) - h( X^T beta)) = 0 $$.
The variance is based on the squared influence functions that are also returned as the iid component. naive.var is variance under known censoring model.
Censoring model may depend on strata (cens.model=~strata(gX)).
References
Blanche PF, Holt A, Scheike T (2022). “On logistic regression with right censored data, with or without competing risks, and its use for estimating treatment effects.” Lifetime data analysis, 29, 441–482. Scheike TH, Zhang MJ, Gerds TA (2008). “Predicting cumulative incidence probability by direct binomial regression.” Biometrika, 95(1), 205–220.
Examples
library(mets)
data(bmt); bmt$time <- bmt$time+runif(408)*0.001
# logistic regresion with IPCW binomial regression
out <- binreg(Event(time,cause)~tcell+platelet,bmt,time=50)
summary(out)
#> n events
#> 408 160
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -0.180332 0.126755 -0.428766 0.068103 0.1548
#> tcell -0.418194 0.345422 -1.095208 0.258820 0.2260
#> platelet -0.437667 0.240973 -0.909965 0.034630 0.0693
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> (Intercept) 0.83499 0.65131 1.0705
#> tcell 0.65823 0.33447 1.2954
#> platelet 0.64554 0.40254 1.0352
#>
#>
head(iid(out))
#> [,1] [,2] [,3]
#> [1,] -0.006946408 0.004004252 0.006177039
#> [2,] -0.006946408 0.004004252 0.006177039
#> [3,] -0.006946408 0.004004252 0.006177039
#> [4,] -0.006946408 0.004004252 0.006177039
#> [5,] -0.006946408 0.004004252 0.006177039
#> [6,] -0.006946408 0.004004252 0.006177039
predict(out,data.frame(tcell=c(0,1),platelet=c(1,1)),se=TRUE)
#> pred se lower upper
#> 1 0.3502366 0.04847385 0.2552279 0.4452454
#> 2 0.2618851 0.06969063 0.1252915 0.3984788
outs <- binreg(Event(time,cause)~tcell+platelet,bmt,time=50,cens.model=~strata(tcell,platelet))
summary(outs)
#> n events
#> 408 160
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -0.180703 0.127413 -0.430429 0.069022 0.1561
#> tcell -0.365924 0.350632 -1.053150 0.321302 0.2967
#> platelet -0.433487 0.240270 -0.904408 0.037433 0.0712
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> (Intercept) 0.83468 0.65023 1.0715
#> tcell 0.69356 0.34884 1.3789
#> platelet 0.64824 0.40478 1.0381
#>
#>
## glm with IPCW weights
outl <- logitIPCW(Event(time,cause)~tcell+platelet,bmt,time=50)
summary(outl)
#> n events
#> 408 160
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -0.241521 0.131457 -0.499171 0.016129 0.0662
#> tcell -0.344491 0.368376 -1.066494 0.377513 0.3497
#> platelet -0.292933 0.262665 -0.807747 0.221881 0.2647
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> (Intercept) 0.78543 0.60703 1.0163
#> tcell 0.70858 0.34421 1.4587
#> platelet 0.74607 0.44586 1.2484
#>
#>
##########################################
### risk-ratio of different causes #######
##########################################
data(bmt)
bmt$id <- 1:nrow(bmt)
bmt$status <- bmt$cause
bmt$strata <- 1
bmtdob <- bmt
bmtdob$strata <-2
bmtdob <- dtransform(bmtdob,status=1,cause==2)
bmtdob <- dtransform(bmtdob,status=2,cause==1)
###
bmtdob <- rbind(bmt,bmtdob)
dtable(bmtdob,cause+status~strata)
#> strata: 1
#>
#> status 0 1 2
#> cause
#> 0 160 0 0
#> 1 0 161 0
#> 2 0 0 87
#> ------------------------------------------------------------
#> strata: 2
#>
#> status 0 1 2
#> cause
#> 0 160 0 0
#> 1 0 0 161
#> 2 0 87 0
cif1 <- cif(Event(time,cause)~+1,bmt,cause=1)
cif2 <- cif(Event(time,cause)~+1,bmt,cause=2)
plot(cif1)
plot(cif2,add=TRUE,col=2)
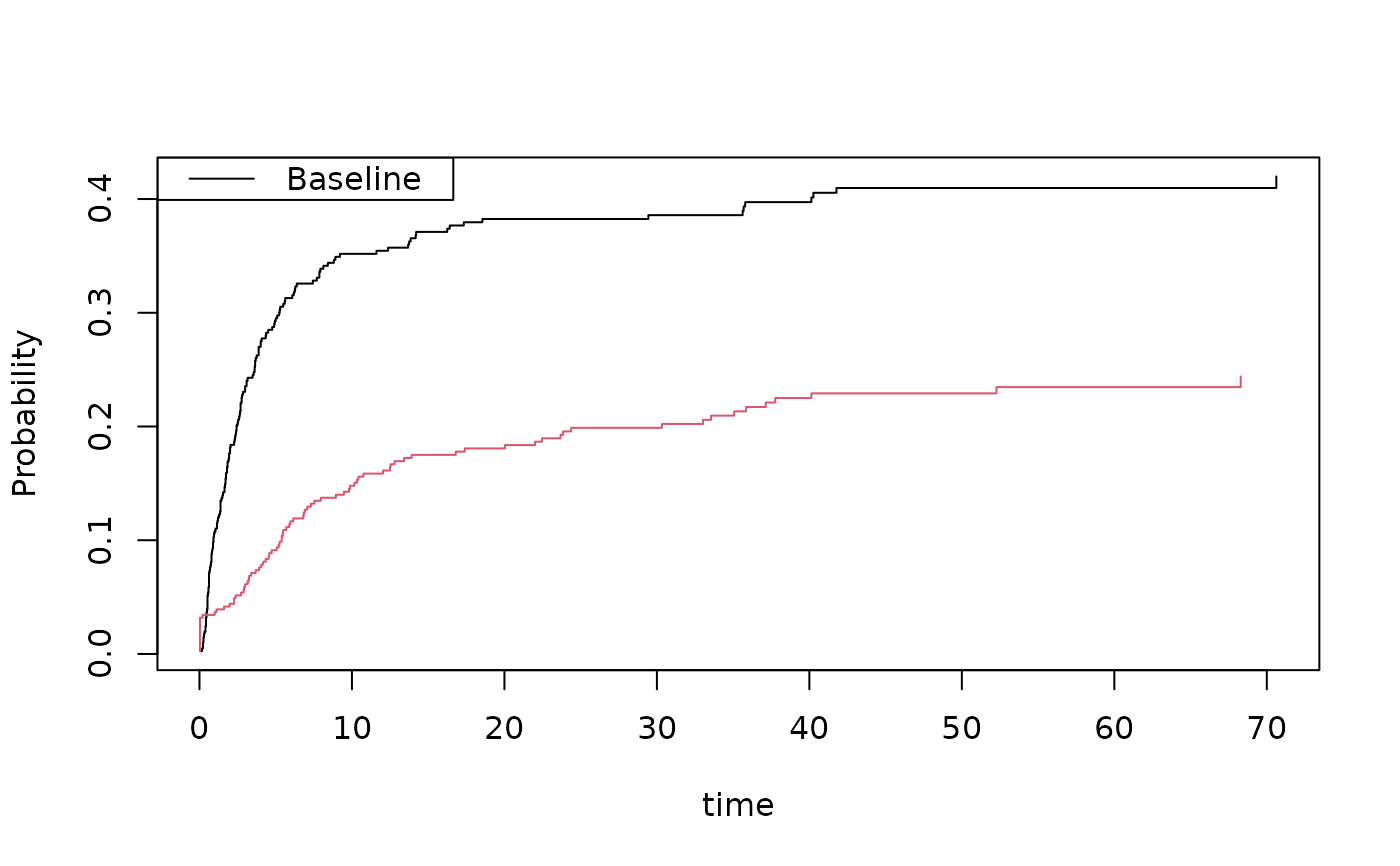cifs1 <- binreg(Event(time,cause)~tcell+platelet+age,bmt,cause=1,time=50)
cifs2 <- binreg(Event(time,cause)~tcell+platelet+age,bmt,cause=2,time=50)
summary(cifs1)
#> n events
#> 408 160
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -0.198947 0.130987 -0.455677 0.057782 0.1288
#> tcell -0.636947 0.356604 -1.335878 0.061983 0.0741
#> platelet -0.344912 0.246013 -0.827089 0.137265 0.1609
#> age 0.437244 0.107266 0.227007 0.647481 0.0000
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> (Intercept) 0.81959 0.63402 1.0595
#> tcell 0.52890 0.26293 1.0639
#> platelet 0.70828 0.43732 1.1471
#> age 1.54843 1.25484 1.9107
#>
#>
summary(cifs2)
#> n events
#> 408 85
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> (Intercept) -1.322081 0.157783 -1.631329 -1.012832 0.0000
#> tcell 0.746834 0.352260 0.056416 1.437252 0.0340
#> platelet -0.019142 0.276984 -0.562021 0.523738 0.9449
#> age -0.072139 0.141687 -0.349842 0.205563 0.6107
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> (Intercept) 0.26658 0.19567 0.3632
#> tcell 2.11031 1.05804 4.2091
#> platelet 0.98104 0.57006 1.6883
#> age 0.93040 0.70480 1.2282
#>
#>
cifdob <- binreg(Event(time,status)~-1+factor(strata)+
tcell*factor(strata)+platelet*factor(strata)+age*factor(strata)
+cluster(id),bmtdob,cause=1,time=50,cens.model=~strata(strata))
summary(cifdob)
#> n events
#> 816 245
#>
#> 408 clusters
#> coeffients:
#> Estimate Std.Err 2.5% 97.5% P-value
#> factor(strata)1 -0.198947 0.130987 -0.455677 0.057782 0.1288
#> factor(strata)2 -1.322081 0.157783 -1.631329 -1.012832 0.0000
#> tcell -0.636947 0.356604 -1.335878 0.061983 0.0741
#> platelet -0.344912 0.246013 -0.827089 0.137265 0.1609
#> age 0.437244 0.107266 0.227007 0.647481 0.0000
#> factor(strata)2:tcell 1.383781 0.600927 0.205986 2.561577 0.0213
#> factor(strata)2:platelet 0.325770 0.432013 -0.520959 1.172500 0.4508
#> factor(strata)2:age -0.509383 0.208101 -0.917254 -0.101513 0.0144
#>
#> exp(coeffients):
#> Estimate 2.5% 97.5%
#> factor(strata)1 0.81959 0.63402 1.0595
#> factor(strata)2 0.26658 0.19567 0.3632
#> tcell 0.52890 0.26293 1.0639
#> platelet 0.70828 0.43732 1.1471
#> age 1.54843 1.25484 1.9107
#> factor(strata)2:tcell 3.98996 1.22874 12.9562
#> factor(strata)2:platelet 1.38510 0.59395 3.2301
#> factor(strata)2:age 0.60087 0.39961 0.9035
#>
#>
head(iid(cifdob))
#> [,1] [,2] [,3] [,4] [,5] [,6]
#> 1 -0.007447571 0.01776726 0.004626980 0.006532086 -0.0006994667 -0.01601858
#> 2 -0.007988246 0.01802853 0.006444080 0.006743734 -0.0035442243 -0.02069211
#> 3 -0.008864645 0.01851042 0.010424440 0.006903340 -0.0101076390 -0.03003705
#> 4 -0.008835416 0.01849245 0.010262329 0.006903222 -0.0098333568 -0.02967265
#> 5 -0.007126560 0.01761890 0.003707153 0.006378236 0.0006895580 -0.01349320
#> 6 -0.009148217 0.01869572 0.012152107 0.006877028 -0.0130608526 -0.03386034
#> [,7] [,8]
#> 1 -0.02078114 0.0033123348
#> 2 -0.01975211 0.0112638920
#> 3 -0.01757153 0.0274275718
#> 4 -0.01765988 0.0267910710
#> 5 -0.02132293 -0.0009455222
#> 6 -0.01662766 0.0341341628
newdata <- data.frame(tcell=1,platelet=1,age=0,strata=1:2,id=1)
riskratio <- function(p) {
cifdob$coef <- p
p <- predict(cifdob,newdata,se=0)
return(p[1]/p[2])
}
lava::estimate(cifdob,f=riskratio)
#> Estimate Std.Err 2.5% 97.5% P-value
#> p1 0.6605 0.2738 0.1239 1.197 0.01585
predict(cifdob,newdata)
#> pred se lower upper
#> 1 0.2349072 0.06592758 0.1056892 0.3641253
#> 2 0.3556286 0.07421505 0.2101671 0.5010901
(p1 <- predict(cifs1,newdata))
#> pred se lower upper
#> 1 0.2349072 0.06592758 0.1056892 0.3641253
#> 2 0.2349072 0.06592758 0.1056892 0.3641253
(p2 <- predict(cifs2,newdata))
#> pred se lower upper
#> 1 0.3556286 0.07421505 0.2101671 0.5010901
#> 2 0.3556286 0.07421505 0.2101671 0.5010901
p1[1,1]/p2[1,1]
#> [1] 0.6605409