Estimation of twostage model with cluster truncation in bivariate situation

Usage

twin.clustertrunc(
  survformula,
  data = parent.frame(),
  theta.des = NULL,
  clusters = NULL,
  var.link = 1,
  Nit = 10,
  final.fitting = FALSE,
  ...
)

Arguments

survformula: Formula with survival model aalen or cox.aalen, some limitiation on model specification due to call of fast.reshape (so for example interactions and * and : do not work here, expand prior to call)
data: Data frame
theta.des: design for dependence parameters in two-stage model
clusters: clustering variable for twins
var.link: exp link for theta
Nit: number of iteration
final.fitting: TRUE to do final estimation with SE and ... arguments for marginal models
...: Additional arguments to lower level functions

Author

Thomas Scheike

Examples

library("timereg")
data(diabetes)
v <- diabetes$time*runif(nrow(diabetes))*rbinom(nrow(diabetes),1,0.5)
diabetes$v <- v

aout <- twin.clustertrunc(Surv(v,time,status)~1+treat+adult,
     data=diabetes,clusters="id")
aout$two        ## twostage output
#> 
#> Dependence parameter for Clayton-Oakes model
#> Variance of Gamma distributed random effects 
#> With log-link 
#> $estimates
#>              log-Coef.        SE          z     P-val Kendall tau         SE
#> dependence1 -0.1874448 0.3183693 -0.5887653 0.5560188   0.2930551 0.06595778
#> 
#> $vargam
#>             Estimate Std.Err   2.5% 97.5%  P-value
#> dependence1   0.8291   0.264 0.3117 1.346 0.001684
#> 
#> $type
#> [1] "clayton.oakes"
#> 
#> attr(,"class")
#> [1] "summary.mets.twostage"
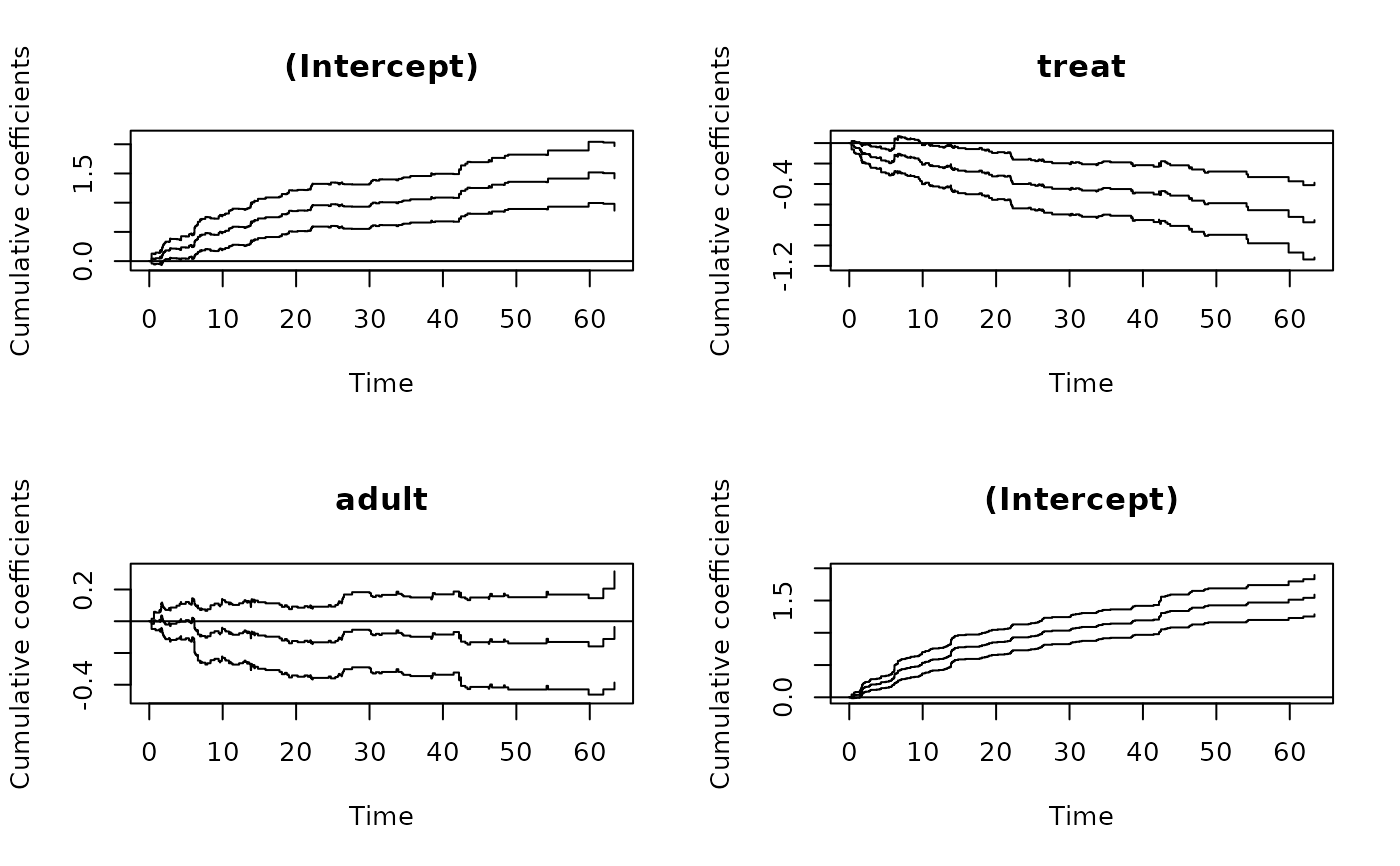
par(mfrow=c(2,2))
plot(aout$marg) ## marginal model output

out <- twin.clustertrunc(Surv(v,time,status)~1+prop(treat)+prop(adult),
     data=diabetes,clusters="id")
out$two        ## twostage output
#> 
#> Dependence parameter for Clayton-Oakes model
#> Variance of Gamma distributed random effects 
#> With log-link 
#> $estimates
#>               log-Coef.        SE          z     P-val Kendall tau         SE
#> dependence1 -0.06020013 0.2998662 -0.2007567 0.8408889   0.3200924 0.06526085
#> 
#> $vargam
#>             Estimate Std.Err   2.5% 97.5%   P-value
#> dependence1   0.9416  0.2823 0.3882 1.495 0.0008535
#> 
#> $type
#> [1] "clayton.oakes"
#> 
#> attr(,"class")
#> [1] "summary.mets.twostage"
plot(out$marg) ## marginal model output