Simulation of recurrent events data based on cumulative hazards: Two-stage model

Simulation of recurrent events data based on cumulative hazards

Usage

simRecurrentTS(
  n,
  cumhaz,
  cumhaz2,
  death.cumhaz = NULL,
  nu = rep(1, 3),
  share1 = 0.3,
  vargamD = 2,
  vargam12 = 0.5,
  gap.time = FALSE,
  max.recurrent = 100,
  cens = NULL,
  ...
)

Arguments

n

number of id's

cumhaz

cumulative hazard of recurrent events

cumhaz2

cumulative hazard of recurrent events of type 2

death.cumhaz

cumulative hazard of death

nu

powers of random effects where nu > -1/shape

share1

how random effect for death splits into two parts

vargamD

variance of random effect for death

vargam12

shared random effect for N1 and N2

gap.time

if true simulates gap-times with specified cumulative hazard

max.recurrent

limits number recurrent events to 100

cens

rate of censoring exponential distribution

...

Additional arguments to lower level funtions

Details

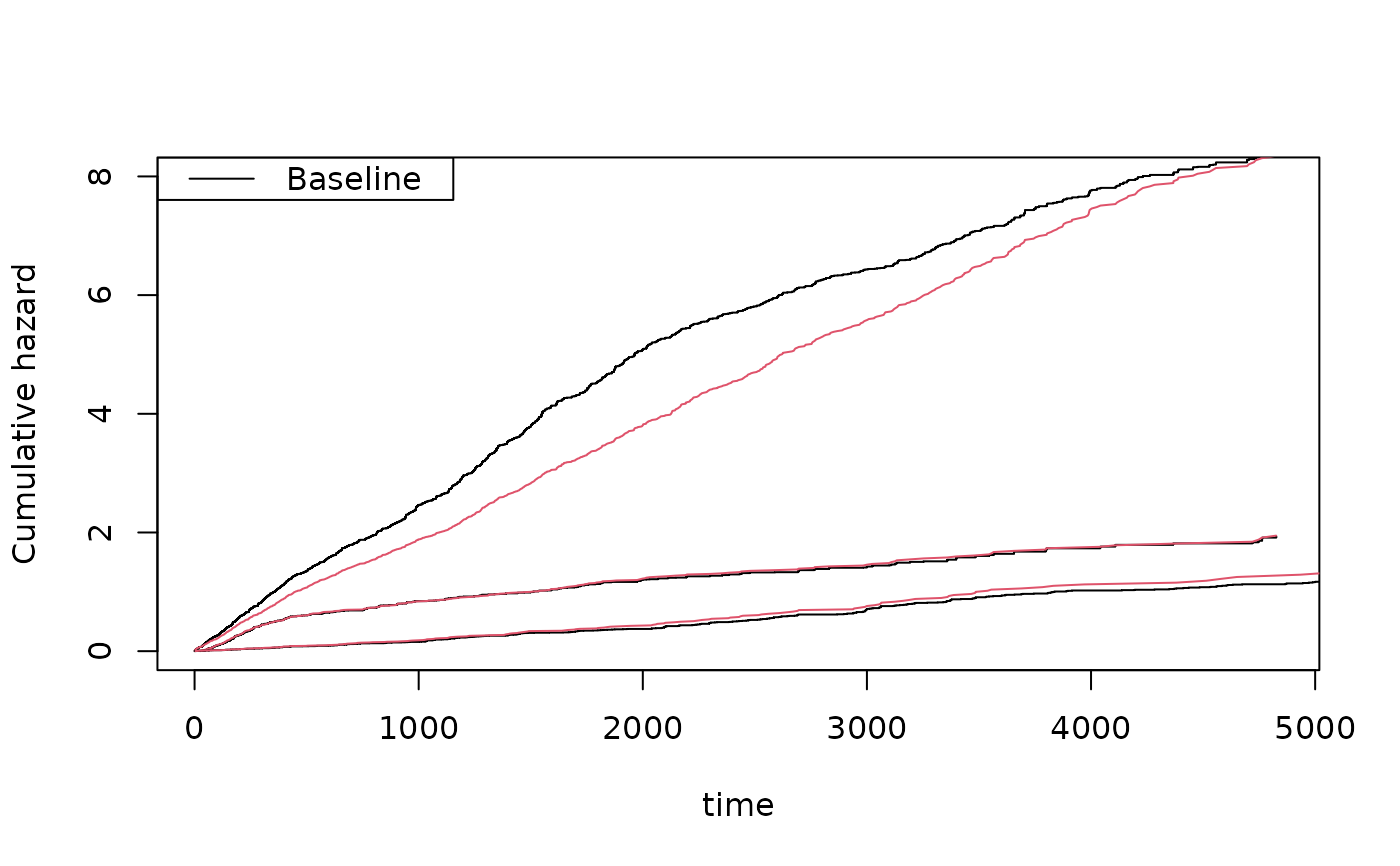
Model is constructed such that marginals are on specified form by linear approximations of cumulative hazards that are on a specific form to make them equivalent to marginals after integrating out over survivors. Therefore E(dN_1 | D>t) = cumhaz, E(dN_2 | D>t) = cumhaz2, and hazard of death is death.cumhazard

Must give hazard of death and two recurrent events. Hazard of death is death.cumhazard two event types and their dependence can be specified but the two recurrent events need to share random effect.

Random effect for death Z.death=(Zd1+Zd2), Z1=(Zd1^nu1) Z12, Z2=(Zd2^nu2) Z12^nu3 $$Z.death=Zd1+Zd2$$ gamma distributions $$Zdj$$ gamma distribution with mean parameters (sharej), vargamD, share2=1-share1 $$Z12$$ gamma distribution with mean 1 and variance vargam12

Author

Thomas Scheike

Examples

########################################
## getting some rates to mimick 
########################################
data(CPH_HPN_CRBSI)
dr <- CPH_HPN_CRBSI$terminal
base1 <- CPH_HPN_CRBSI$crbsi 
base4 <- CPH_HPN_CRBSI$mechanical

rr <- simRecurrentTS(1000,base1,base4,death.cumhaz=dr)
dtable(rr,~death+status)
#> 
#>       status    0    1    2
#> death                      
#> 0             138 2394  384
#> 1             861    0    0
showfitsim(causes=2,rr,dr,base1,base4)