Estimation of probability of more that k events for recurrent events process

Estimation of probability of more that k events for recurrent events process where there is terminal event, based on this also estimate of variance of recurrent events. The estimator is based on cumulative incidence of exceeding "k" events. In contrast the probability of exceeding k events can also be computed as a counting process integral.

Usage

prob.exceed.recurrent(
  formula,
  data,
  cause = 1,
  death.code = 2,
  cens.code = 0,
  exceed = NULL,
  marks = NULL,
  all.cifs = FALSE,
  return.data = FALSE,
  conf.type = c("log", "plain"),
  level = 0.95,
  ...
)

Arguments

formula

formula

data

data-frame

cause

of interest

death.code

for status

cens.code

censoring codes

exceed

values (if not given then all observed values)

marks

may be give for jump-times and then exceed values needs to be specified

all.cifs

if true then returns list of all fitted objects in cif.exceed

return.data

if true then returns list of data for fitting the different excess thresholds

conf.type

type of confidence interval c("log","plain")

level

of confidence intervals default is 0.95

...

Additional arguments to lower level funtions

References

Scheike, Eriksson, Tribler (2019), The mean, variance and correlation for bivariate recurrent events with a terminal event, JRSS-C

Author

Thomas Scheike

Examples

library(mets)
data(hfactioncpx12)
dtable(hfactioncpx12,~status)
#> 
#> status
#>    0    1    2 
#>  617 1391  124 
#> 

oo <- prob.exceed.recurrent(Event(entry,time,status)~cluster(id),
        hfactioncpx12,cause=1,death.code=2)
plot(oo)

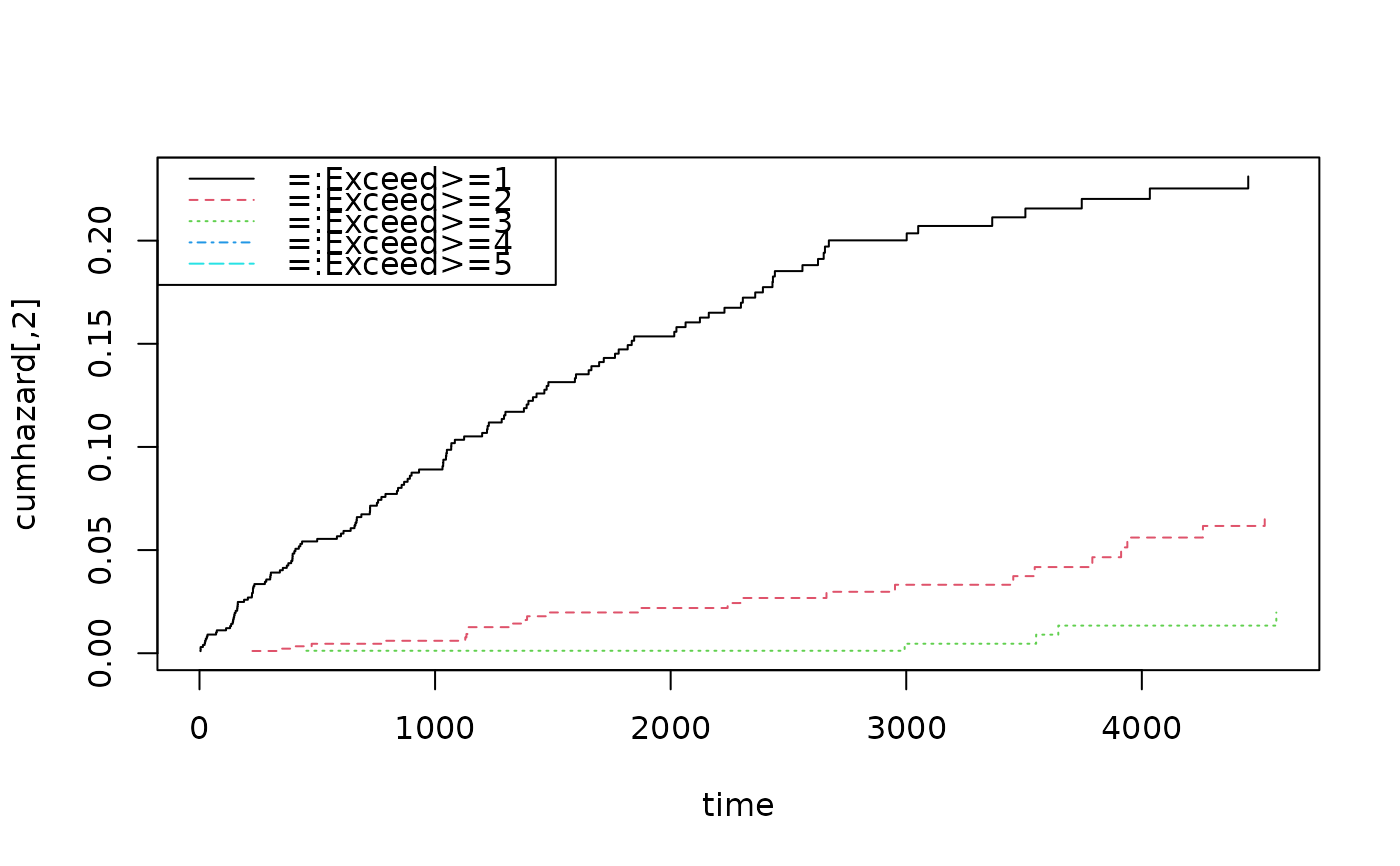summary(oo,times=c(1,2,5))
#> $prob
#>      times                 N<1 exceed>=1 exceed>=2 exceed>=3  exceed>=4
#> [1,]     1 0.9978807 0.5747460 0.4252540 0.2008652 0.1012955 0.04794006
#> [2,]     2 1.9967128 0.3925156 0.6074844 0.3509483 0.2205076 0.13989818
#> [3,]     5 3.9793816 0.1925999 0.8074001 0.5477499 0.3899373 0.29900312
#>       exceed>=5  exceed>=6   exceed>=7
#> [1,] 0.03153223 0.01371012 0.008229099
#> [2,] 0.10092792 0.05533511 0.035595440
#> [3,] 0.19615192 0.14357991 0.103037717
#> 
#> $se
#>      times                  N<1  exceed>=1  exceed>=2  exceed>=3   exceed>=4
#> [1,]     1 0.9978807 0.01827977 0.01827977 0.01481729 0.01116527 0.007907269
#> [2,]     2 1.9967128 0.01862412 0.01862412 0.01832598 0.01592337 0.013395849
#> [3,]     5 3.9793816 0.02129779 0.02129779 0.02413438 0.02515176 0.024909447
#>        exceed>=5   exceed>=6   exceed>=7
#> [1,] 0.006470709 0.004305759 0.003345689
#> [2,] 0.011774638 0.008883381 0.007151615
#> [3,] 0.020706361 0.019083117 0.016923719
#> 
#> $lower
#>      times                                                             
#> [1,]     1 0.9978807 0.6091060 0.3908940 0.1738256 0.08161439 0.0346977
#> [2,]     2 1.9967128 0.4279431 0.5720569 0.3168070 0.19140637 0.1159594
#> [3,]     5 3.9793816 0.2332821 0.7667179 0.5024323 0.34362952 0.2539590
#>                                        
#> [1,] 0.02109017 0.007408243 0.003709206
#> [2,] 0.08029840 0.040397144 0.024009120
#> [3,] 0.15949140 0.110652445 0.074677237
#> 
#> $upper
#>      times                                                             
#> [1,]     1 0.9978807 0.5373658 0.4626342 0.2321109 0.1257227 0.06623635
#> [2,]     2 1.9967128 0.3548940 0.6451060 0.3887690 0.2540334 0.16877894
#> [3,]     5 3.9793816 0.1497591 0.8502409 0.5971550 0.4424855 0.35203666
#>                                     
#> [1,] 0.0471443 0.02537272 0.01825676
#> [2,] 0.1268574 0.07579680 0.05277309
#> [3,] 0.2412392 0.18630579 0.14216877
#>