Discrete time to event interval censored data — interval.logitsurv.discrete • mets

We consider the cumulative odds model $$ P(T \leq t | x) = \frac{G(t) \exp(x \beta) }{1 + G(t) exp( x \beta) } $$ or equivalently $$ logit(P(T \leq t | x)) = log(G(t)) + x \beta $$ and we can thus also compute the probability of surviving $$ P(T >t | x) = \frac{1}{1 + G(t) exp( x \beta) } $$

Usage

interval.logitsurv.discrete(
  formula,
  data,
  beta = NULL,
  no.opt = FALSE,
  method = "NR",
  stderr = TRUE,
  weights = NULL,
  offsets = NULL,
  exp.link = 1,
  increment = 1,
  ...
)

Arguments

formula: formula
data: data
beta: starting values
no.opt: optimization TRUE/FALSE
method: NR, nlm
stderr: to return only estimate
weights: weights following id for GLM
offsets: following id for GLM
exp.link: parametrize increments exp(alpha) > 0
increment: using increments dG(t)=exp(alpha) as parameters
...: Additional arguments to lower level funtions lava::NR optimizer or nlm

Details

The baseline $G(t)$ is written as $cumsum(exp(\alpha))$ and this is not the standard parametrization that takes log of $G(t)$ as the parameters. Note that the regression coefficients are describing the probability of dying before or at time t.

Input are intervals given by ]t_l,t_r] where t_r can be infinity for right-censored intervals When truly discrete ]0,1] will be an observation at 1, and ]j,j+1] will be an observation at j+1. Can be used for fitting the usual ordinal regression model (with logit link) that in contrast, however, describes the probibility of surviving time t (thus leads to -beta).

Likelihood is maximized: $$ \prod P(T_i >t_{il} | x) - P(T_i> t_{ir}| x) $$

Author

Thomas Scheike

Examples

library(mets)
data(ttpd) 
dtable(ttpd,~entry+time2)
#> 
#>       time2   1   2   3   4   5   6 Inf
#> entry                                  
#> 0           316   0   0   0   0   0   0
#> 1             0 133   0   0   0   0   0
#> 2             0   0 150   0   0   0   0
#> 3             0   0   0  23   0   0   0
#> 4             0   0   0   0  90   0   0
#> 5             0   0   0   0   0  68   0
#> 6             0   0   0   0   0   0 220

out <- interval.logitsurv.discrete(Interval(entry,time2)~X1+X2+X3+X4,ttpd)
summary(out)
#> $baseline
#>       Estimate Std.Err   2.5%   97.5%   P-value
#> time1  -2.0064  0.1523 -2.305 -1.7079 1.273e-39
#> time2  -2.1749  0.1599 -2.488 -1.8614 4.118e-42
#> time3  -1.4581  0.1544 -1.761 -1.1554 3.636e-21
#> time4  -2.9260  0.2453 -3.407 -2.4453 8.379e-33
#> time5  -1.2051  0.1706 -1.539 -0.8706 1.633e-12
#> time6  -0.9102  0.1860 -1.275 -0.5457 9.843e-07
#> 
#> $logor
#>    Estimate Std.Err    2.5%  97.5%   P-value
#> X1   0.9913  0.1179 0.76024 1.2223 4.100e-17
#> X2   0.6962  0.1162 0.46847 0.9238 2.064e-09
#> X3   0.3466  0.1159 0.11941 0.5738 2.788e-03
#> X4   0.3223  0.1151 0.09668 0.5478 5.111e-03
#> 
#> $or
#>    Estimate     2.5%    97.5%
#> X1 2.694610 2.138791 3.394874
#> X2 2.006032 1.597554 2.518953
#> X3 1.414239 1.126834 1.774950
#> X4 1.380231 1.101503 1.729490
#> 
head(iid(out)) 
#>            [,1]         [,2]          [,3]          [,4]          [,5]
#> 1  0.0045687959  0.004769499  0.0053427163  0.0059138018  0.0066308444
#> 2  0.0016959549  0.002038630  0.0025477402  0.0029776943 -0.0102830496
#> 3  0.0045687959  0.004769499  0.0053427163  0.0059138018  0.0066308444
#> 4  0.0027545442 -0.006047556 -0.0007244072 -0.0006949805 -0.0006704063
#> 5 -0.0002919658 -0.008889214 -0.0026820744 -0.0026532556 -0.0026268232
#> 6  0.0001497624 -0.008530642 -0.0033151419 -0.0032325395 -0.0031636812
#>            [,6]          [,7]          [,8]          [,9]         [,10]
#> 1  0.0081721788 -0.0033482398 -0.0034168560  0.0034308192 -0.0034212419
#> 2 -0.0012875717 -0.0007883982 -0.0005310631 -0.0004080546 -0.0000776067
#> 3  0.0081721788 -0.0033482398 -0.0034168560  0.0034308192 -0.0034212419
#> 4 -0.0006379316  0.0003557924  0.0007697270  0.0008855193 -0.0013506040
#> 5 -0.0025608456 -0.0026170215  0.0016772465  0.0020412533  0.0017043055
#> 6 -0.0030621110  0.0015290328  0.0016662399  0.0020179143  0.0017471657

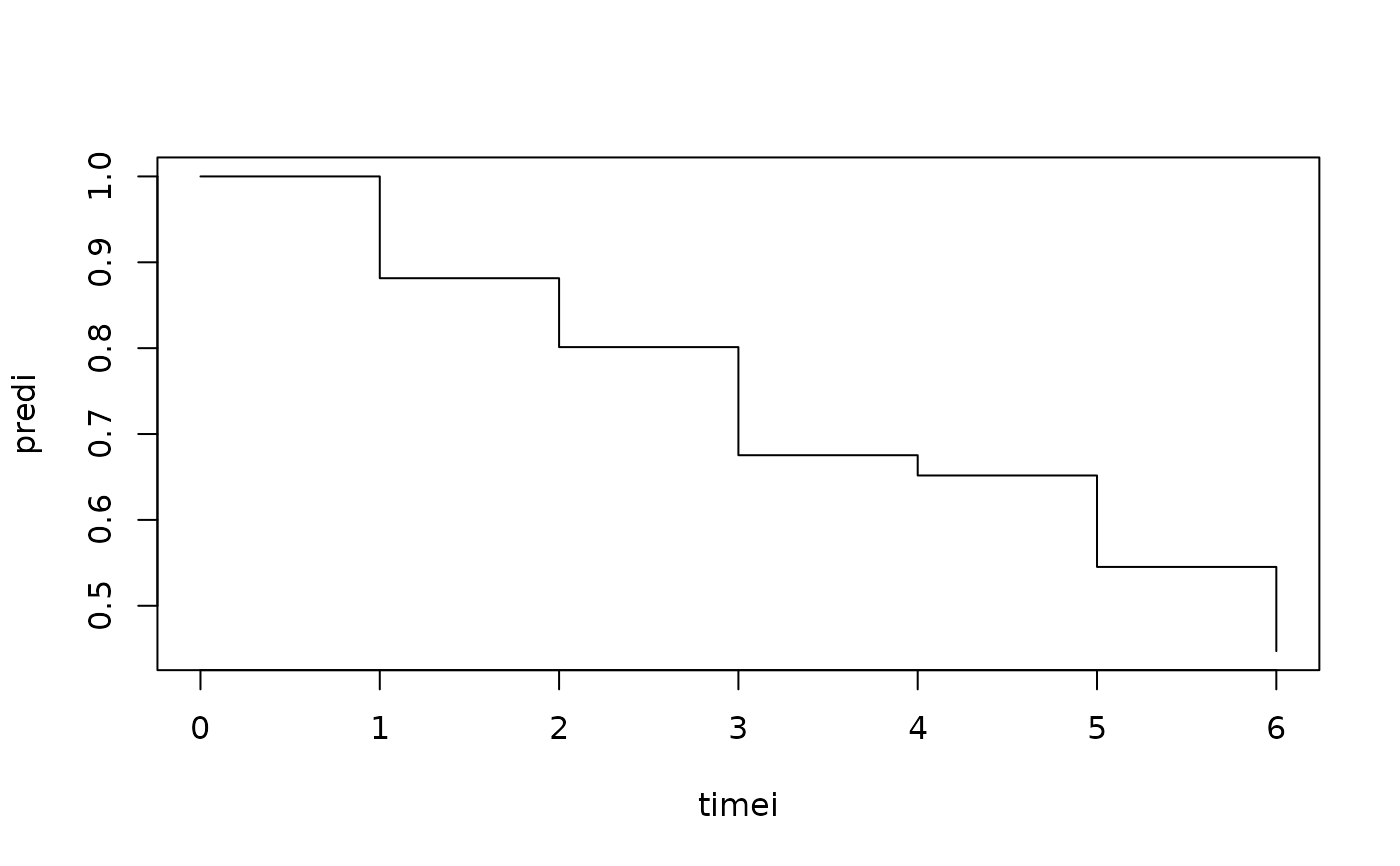
pred <- predictlogitSurvd(out,se=FALSE)
plotSurvd(pred)


ttpd <- dfactor(ttpd,fentry~entry)
out <- cumoddsreg(fentry~X1+X2+X3+X4,ttpd)
summary(out)
#> $baseline
#>       Estimate Std.Err   2.5%   97.5%   P-value
#> time1  -2.0064  0.1523 -2.305 -1.7079 1.273e-39
#> time2  -2.1749  0.1599 -2.488 -1.8614 4.118e-42
#> time3  -1.4581  0.1544 -1.761 -1.1554 3.636e-21
#> time4  -2.9260  0.2453 -3.407 -2.4453 8.379e-33
#> time5  -1.2051  0.1706 -1.539 -0.8706 1.633e-12
#> time6  -0.9102  0.1860 -1.275 -0.5457 9.843e-07
#> 
#> $logor
#>    Estimate Std.Err    2.5%  97.5%   P-value
#> X1   0.9913  0.1179 0.76024 1.2223 4.100e-17
#> X2   0.6962  0.1162 0.46847 0.9238 2.064e-09
#> X3   0.3466  0.1159 0.11941 0.5738 2.788e-03
#> X4   0.3223  0.1151 0.09668 0.5478 5.111e-03
#> 
#> $or
#>    Estimate     2.5%    97.5%
#> X1 2.694610 2.138791 3.394874
#> X2 2.006032 1.597554 2.518953
#> X3 1.414239 1.126834 1.774950
#> X4 1.380231 1.101503 1.729490
#> 
head(iid(out)) 
#>            [,1]         [,2]          [,3]          [,4]          [,5]
#> 1  0.0045687959  0.004769499  0.0053427163  0.0059138018  0.0066308444
#> 2  0.0016959549  0.002038630  0.0025477402  0.0029776943 -0.0102830496
#> 3  0.0045687959  0.004769499  0.0053427163  0.0059138018  0.0066308444
#> 4  0.0027545442 -0.006047556 -0.0007244072 -0.0006949805 -0.0006704063
#> 5 -0.0002919658 -0.008889214 -0.0026820744 -0.0026532556 -0.0026268232
#> 6  0.0001497624 -0.008530642 -0.0033151419 -0.0032325395 -0.0031636812
#>            [,6]          [,7]          [,8]          [,9]         [,10]
#> 1  0.0081721788 -0.0033482398 -0.0034168560  0.0034308192 -0.0034212419
#> 2 -0.0012875717 -0.0007883982 -0.0005310631 -0.0004080546 -0.0000776067
#> 3  0.0081721788 -0.0033482398 -0.0034168560  0.0034308192 -0.0034212419
#> 4 -0.0006379316  0.0003557924  0.0007697270  0.0008855193 -0.0013506040
#> 5 -0.0025608456 -0.0026170215  0.0016772465  0.0020412533  0.0017043055
#> 6 -0.0030621110  0.0015290328  0.0016662399  0.0020179143  0.0017471657