Regression model for binomial data with unkown group of immortals (zero-inflated binomial regression)
zibreg(
formula,
formula.p = ~1,
data,
family = stats::binomial(),
offset = NULL,
start,
var = "hessian",
...
)Arguments
- formula
Formula specifying
- formula.p
Formula for model of disease prevalence
- data
data frame
- family
Distribution family (see the help page
family)- offset
Optional offset
- start
Optional starting values
- var
Type of variance (robust, expected, hessian, outer)
- ...
Additional arguments to lower level functions
Examples
## Simulation
n <- 2e3
x <- runif(n,0,20)
age <- runif(n,10,30)
z0 <- rnorm(n,mean=-1+0.05*age)
z <- cut(z0,breaks=c(-Inf,-1,0,1,Inf))
p0 <- lava:::expit(model.matrix(~z+age) %*% c(-.4, -.4, 0.2, 2, -0.05))
y <- (runif(n)<lava:::tigol(-1+0.25*x-0*age))*1
u <- runif(n)<p0
y[u==0] <- 0
d <- data.frame(y=y,x=x,u=u*1,z=z,age=age)
head(d)
#> y x u z age
#> 1 0 1.464937 0 (0,1] 18.21027
#> 2 0 8.471168 0 (-1,0] 24.61046
#> 3 0 10.616487 0 (-Inf,-1] 27.67200
#> 4 1 18.854095 1 (-1,0] 12.28950
#> 5 0 14.244491 0 (-1,0] 16.48295
#> 6 0 14.489812 0 (-1,0] 17.33514
## Estimation
e0 <- zibreg(y~x*z,~1+z+age,data=d)
e <- zibreg(y~x,~1+z+age,data=d)
compare(e,e0)
#>
#> - Likelihood ratio test -
#>
#> data:
#> chisq = 2.4545, df = 6, p-value = 0.8735
#> sample estimates:
#> log likelihood (model 1) log likelihood (model 2)
#> -845.5394 -844.3122
#>
e
#> Estimate 2.5% 97.5% P-value
#> (Intercept) -0.8096962 -1.34568375 -0.27370865 3.067975e-03
#> x 0.2247970 0.06065481 0.38893919 7.269888e-03
#> pr:(Intercept) -0.1388121 -0.78249152 0.50486730 6.725329e-01
#> pr:z(-1,0] -0.3544657 -0.78800432 0.07907295 1.090480e-01
#> pr:z(0,1] 0.4362824 0.02118711 0.85137778 3.939820e-02
#> pr:z(1, Inf] 2.3908142 1.81380254 2.96782578 4.623694e-16
#> pr:age -0.0752326 -0.10102715 -0.04943804 1.087750e-08
#>
#> Prevalence probabilities:
#> Estimate 2.5% 97.5%
#> {(Intercept)} 0.4653526 0.3137832 0.6236025
#> {(Intercept)} + {z(-1,0]} 0.3791217 0.2487184 0.5296910
#> {(Intercept)} + {z(0,1]} 0.5738240 0.4098366 0.7230380
#> {(Intercept)} + {z(1, Inf]} 0.9048231 0.7876751 0.9605714
#> {(Intercept)} + {age} 0.4466922 0.3018984 0.6011322
PD(e0,intercept=c(1,3),slope=c(2,6))
#> Estimate Std.Err 2.5% 97.5%
#> 50% 4.655517 6.753757 -8.581603 17.89264
#> attr(,"b")
#> [1] -0.7921916 0.1701619
B <- rbind(c(1,0,0,0,20),
c(1,1,0,0,20),
c(1,0,1,0,20),
c(1,0,0,1,20))
prev <- summary(e,pr.contrast=B)$prevalence
x <- seq(0,100,length.out=100)
newdata <- expand.grid(x=x,age=20,z=levels(d$z))
fit <- predict(e,newdata=newdata)
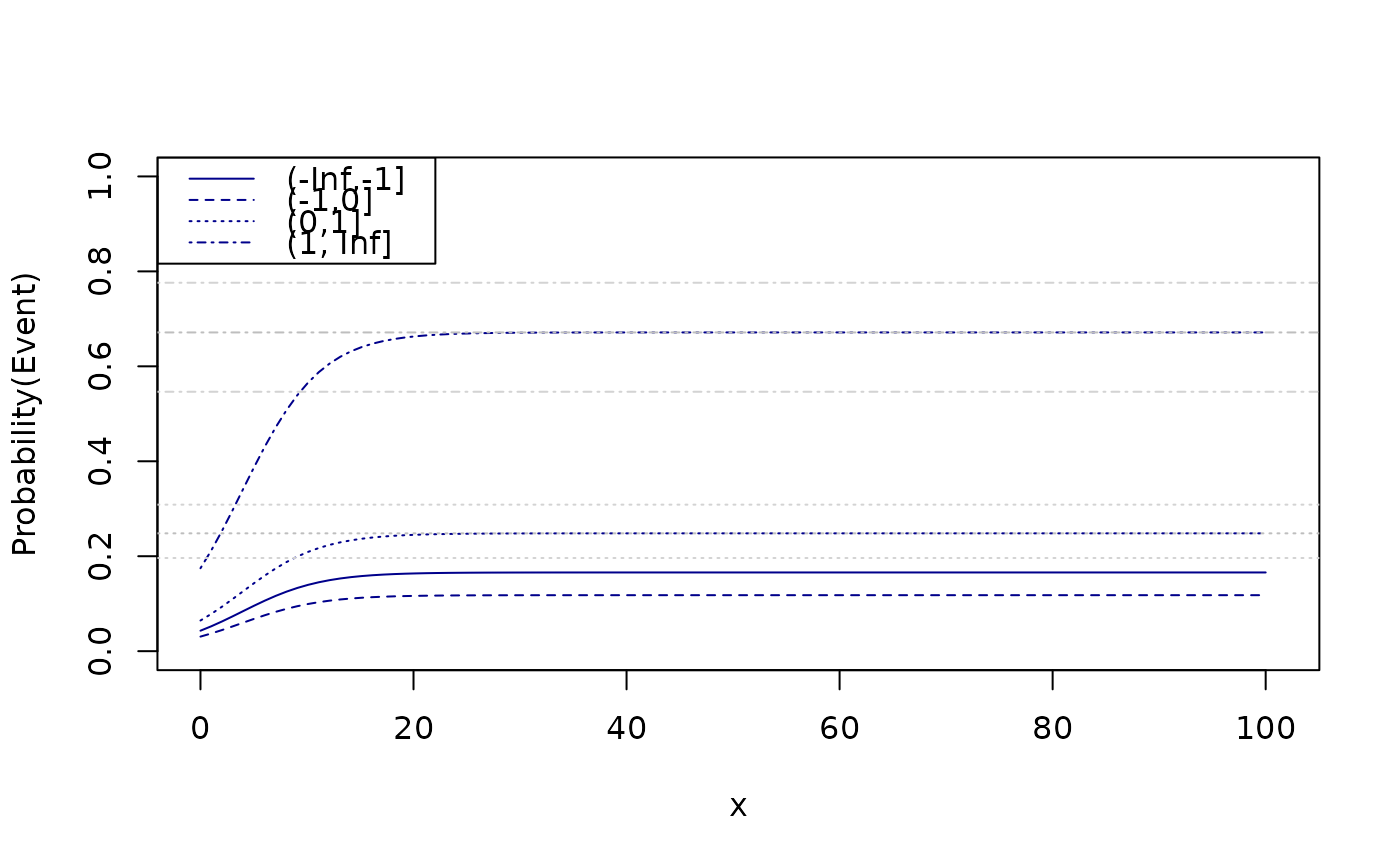
plot(0,0,type="n",xlim=c(0,101),ylim=c(0,1),xlab="x",ylab="Probability(Event)")
count <- 0
for (i in levels(newdata$z)) {
count <- count+1
lines(x,fit[which(newdata$z==i)],col="darkblue",lty=count)
}
abline(h=prev[3:4,1],lty=3:4,col="gray")
abline(h=prev[3:4,2],lty=3:4,col="lightgray")
abline(h=prev[3:4,3],lty=3:4,col="lightgray")
legend("topleft",levels(d$z),col="darkblue",lty=seq_len(length(levels(d$z))))
